Basic Concepts

• In digital signal processing, a "signal" refers to a representation of how a physical phenomenon evolves over time. This means that a signal is a function mapping real numbers (time domain) to real values representing a physical phenomenon.

• In digital signal processing, “processing” refers to either analyzing a signal to extract the information it carries or synthesizing a signal to encode specific information.

• A physical device can sense a continuous (analog) signal, but when it records the signal digitally, it captures only discrete samples in time and amplitude. As a result, it can be difficult to recover the exact underlying function that describes the original physical phenomenon without making certain assumptions, such as the signal being bandlimited.

• A discrete model of reality could offer practical benefits for representing and analyzing the real world.

• Foundational idea in signal processing: the Nyquist-Shannon Sampling theorem.

  • Under appropriate "slowness" conditions for x(t) we have

• Analog signal: to discrete signal

• if the signal is digitized (quantized)

  • The amplitude is rounded to a finite set of levels (e.g., integers 0–255 for 8-bit audio).

  • That’s digital signal processing, a subset of DSP.

  This has advantages of storage, processing, and transmission.

• Analog signal

  • where G: attenuation and sigma is a noise.

Basic concepts of DSP

• Four signal classes

  • finite-length

  • infinite-length: abstract, and good for theorem

  • periodic:

  • finite-support:

• Energy and Power

  • Energy:

  • Power

Digital vs Physical frequency

• Ts: Time in seconds between samples

• periodicity of M samples implies periodicity MTs seconds

• real world frequency = 1/(MTs) Hz

• Example 1: Fs: the number of samples per seconds (it does not matter of periodicity. This is the how fast the data is collected)
  Fs = 48000 => Ts = 1/48000 =0.00002083sec =20.83 μsecs. If the discrete signal repeats itself every M = 110 samples, then periodicity MTs = 0.00229167 seconds. This implies f = 436.36Hz

• Example 2: Fs = 44000 => Ts = 1/44000 =0.0000227. To make A5(880Hz), we need to have periodicity of 50 samples.

• Hm.. I guess given values are the Fs and output would be sound frequency, f in terms of the periodicity of M samples.

  • This implies, given Fs, f(M) = 1/(MTs) = Fs/M.

  • Then, my question is how to change the periodicity?

• Python code of the basic concept

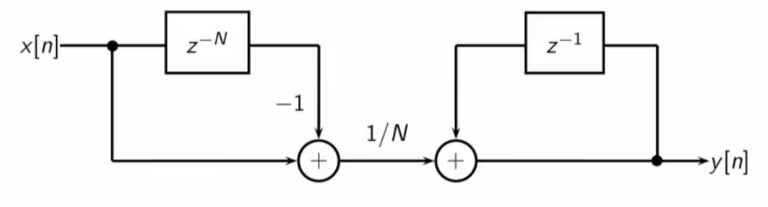
• If x[n] is a delta function, x[n-k] is a k-shifted delta function.

  • , then y[n] is k-periodic delta function.

  • is also a periodic function.

• Simple music sound example in Github

  • control frequency (pitch)

  • control envelop (decay)

  • controls color (timbre)

• Not every sinusoid is periodic in discrete time

  • periodicity. . This implies one point has many names, i.e. .This is called "Aliasing".

  • Aliasing: a phenomenon that occurs when a digital system tries to represent a continuous signal with discrete samples, leading to distortion or misrepresentation of the original signal.

• Moving average

  •