Linear Analog Electric IIR Filters (in github)

• Butterworth Filter : a type of signal filter designed to have the flattest possible frequency response in the passband — meaning it passes signals below a certain cutoff frequency without ripple and attenuates signals above that frequency smoothly.

  • Frequency response: a measure of how well a system, like a speaker or control system, handles a range of input frequencies. The quantitive measure of the magnitude and phase of the output as a function of input frequency.

  • Key properties:

    • Maximally flat magnitude response
      No ripples in the passband or stopband. The gain decreases smoothly.

    • Monotonic roll-off:
      The transition from passband to stopband is smooth and gradual (slower than Chebyshev or elliptic filters).

    • Phase response:

      Non-linear, but smoother than some other IIR filters.

    • Order vs. roll-off:

      The higher the order n, the steeper the transition near the cutoff frequency

  • Frequency Response

    • The magnitude response of an n-th order Butterworth lowpass filter is
      
      
      
      
      
      where w = angular frequency, w_c = cut off frequency, n= order of filter.

  • In the python code,
    b, a = signal.butter(order, cutoff / (fs/2), btype='low')

    • b and a are the coefficients of the filter's transfer function:
      
      
      
      This is a standard IIR difference equation form.
      
      
      
      
      
      FIR difference equation form is
      
      
      

  • Butterworth filter can be used when we want to have smooth, flat response (general-purpose filtering). Most audio or sensor filtering (flat and smooth) can be used for butterworth filter.

• Chebyshev filter: a type of analog or digital filter designed to have a steeper roll-off (transition from passband to stopband) than a Butterworth filter of the same order — but the trade-off is that it allows ripple (oscillation) in either the passband or the stopband, depending on the version.

  • Key properties

    • Faster roll-off, but with ripple (non-flatness)

  • Types

    • Chebyshev Type1: Passband ripple, flat stopband, most common for fast cutoff

    • Chebyshev Type2: Stopband ripple, flat passband, Used when passband flatness is important.

  • Frequency response

    • Magnitude response formaula (low-pass, Type 1):
      
      
      
      
      where C_n = Chebyshev polynomial of order n. \epsilon = ripple factor (larger->more ripple, steeper roll-off, w_c = cutoff frequency)

    • Magnitude response formaula (low-pass, Type 2):
      
      

  • Application:

    • Audio processing: Steeper filtering with minimal delay (e.g., crossover networks)

    • Communication systems: Channel filtering where sharp cutoff is critical

    • Measurement systems: Where noise above a frequency must be strongly attenuated.

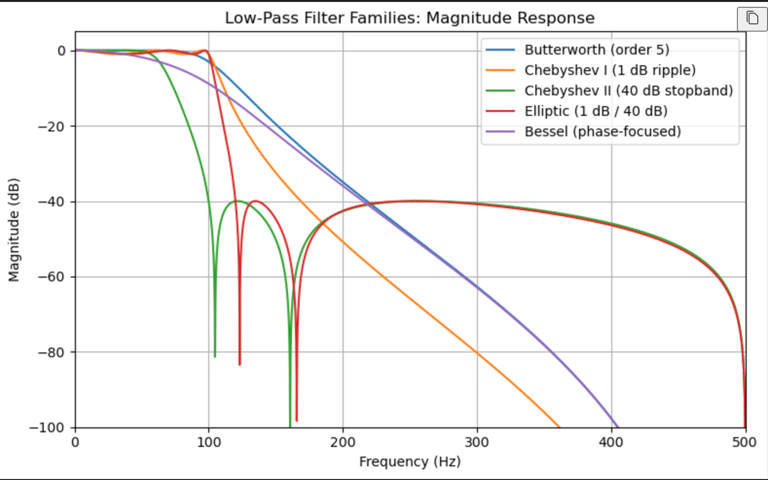
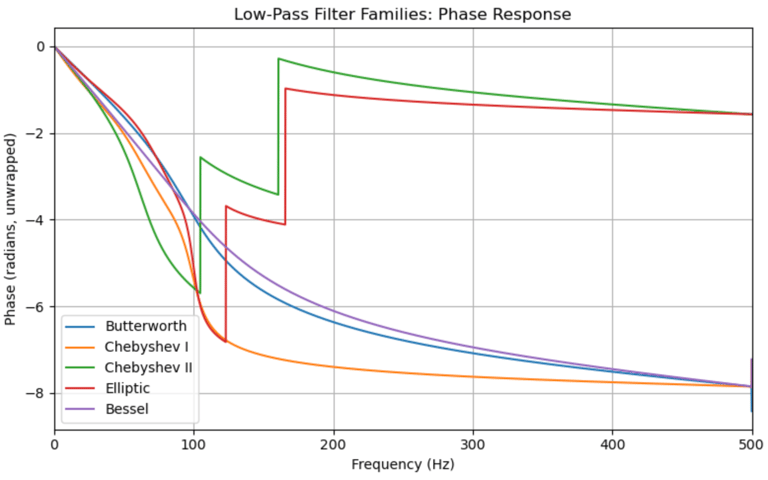
• Elliptic Filter: the sharpest transition between passband and stopband for a given order. It allows ripple in both the passband and the stopband, but the steepest roll-off, the lowest order, and very strong selectivity between passband stopband.

  • Maginitude Response
    
    
    
    
    where \epsilon = ripple factor (controls passband ripple), R_n(\xi, x) = elliptic rational function of order n, \xi = selectivity parameter (related to the stopband ripple), w_c= cutoff frequency.
    

  • Application:

    • Sharpest frequency cutoff for a given order

    • tolerates ripple in both passband stopband

    • efficient filters with minimal computation cost (low order)

    • Digital communication systems (tight bandwidth requirements)

    • Anti-aliasing filters

    • Channel separation in multiband systems

    • Real-time DSP where filter order must be minimized.