Exercise

1. Review of complex numbers

a.

b.

c.

d.

e.

2. Sampling Music.

   A music song recorded in a studio is stored as a digital sequence on a CD. The analog signal representing the

   music is 2 minutes long and is sampled at a frequency fs =44100 s−1. How many samples should be stored

   on the CD?

   Sol)

   This assumes that the audio is mono; for stereo data, there are two independent channels so the number of

   samples is double.

3. Consider the following signal,

   x [n]=δ[n]+2δ[n− 1]+3δ[n− 2]. (1)

   Compute its moving average y [n]=(x [n]+x [n−1]) / 2, where we call x [n]the input and y [n]the output.

   Sol) ...x[-2] = 0, x[-1] = 0, x[0] = 1, x[1] = 2, x[2], = 3, x[3] = 0, x[4] = 0, ....

   Therefore, .... y[-2] = 0, y[-1] = 0, y[0] = 0.5, y[1] = 1.5, y[2] = 2.5, y[3] = 1.5, y[4] = 0, .....

   Otherwise,

4. 
   
   
   
   
   
   
   
   
   
   
   
   Sol)

5. Let {x(k )}k=0,...,N−1 be a basis for a subspace S. Prove that any vector z ∈ S is uniquely represented in this basis.
   Sol) Prove it by contradiction.

6. Consider the four diagonals of a three-dimensional unit cube as vectors in 3. Are they mutually orthogonal?
   Sol)

7. Derive a simple expression for the DFT of the time-reversed signal
   
   
   in terms of the DFT x of signal x.
   Sol )
   
   
   
   
   

   
   
   
   
   
   

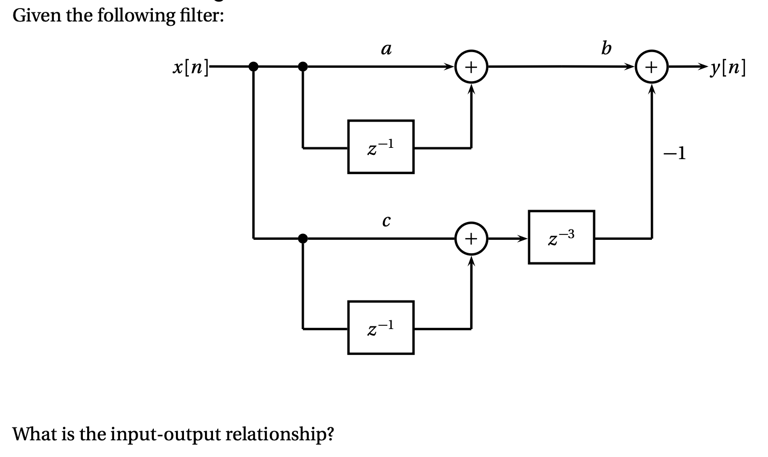
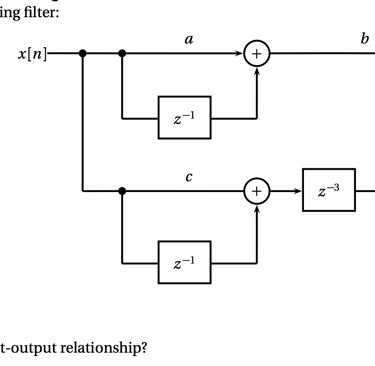
8. Consider a length-N signal. and the corresponding vector of DFT coefficients
   Consider now the length-2N signal obtained by interleaving the values of x with zeros
   Express X2 (the 2N -point DFT of x2) in terms of X.
   Sol)
   
   
   
   
   
   
   
   We need to consider the range of k, 0< k < 2N-1, So
   
   

9. The DFT and IDFT formulas are similar, but not identical. Consider a length-N signal x with x [n], N= 0, . . ., N− 1. What is the length-N signal y [n] obtained as y=DFT{DFT{x}}?

   In other words, what are the effects of applying twice the DFT transform?
   Sol)

10. Consider a sequence x of finite length N . Let X denote the N point DFT of x and define the circular autocorrelation sequence rx as
    
    
    Express rx in terms of X. [Hint: build a signal S[n]=X [n]X ∗[n], compute its inverse DFT and work backwards.]
    Sol)

11. Consider x ∈ C^N with N even and its N - point DFT X. Define an (N/2)-length vector Y as Y[k] = X[2k], k = 0, . . ., N /2− 1. Compute the inverse DFT of Y.
    Sol)

This is the reversed of FFT with one shift

12. Let x [n]and y [n]be two complex-valued sequences and X (e^{jw})and Y (e^{jw})their corresponding DTFTs.

    1. Show that
       
       
       
       where we use the inner products for l2(Z) and L2([-pi,pi]) respectively.

       Pf)
       
       
       
       
       
       
       
       
       

    2. What is the physical meaning of the above formula when x [n]=y [n]?

       Sol) This is the energy conservation in time domain and frequency domain.

13. Derive the time-reverse and time-shift properties of the DTFT.