2. Convolution

   Let x[n] be a discrete-time sequence defined as

for some odd integer M.
(a) Show that x[n] can be expressed as the convolution of two discrete-time sequences x1[n] and x2[n].
Sol) Let

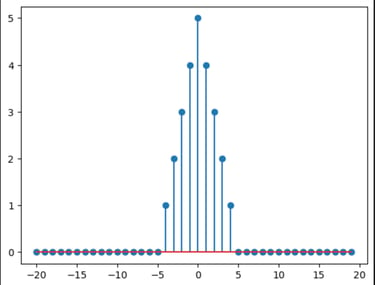
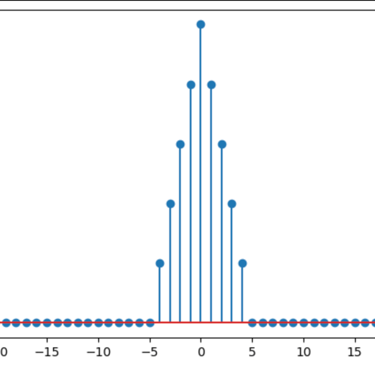
(b) Using the results found in (a), compute the DTFT of x[n]

Sol: By the definition of DTFT,

This does not converge in the ordinary sense. However, from the DTFT of r^n u[n] function we could get

If r goes to 1(-), then it becomes

Since the sum diverges at \omega = 0, we need to add \delta[n]. There is a consideration of the coefficient. For the DTFT of a constant function is

Let's think about u[n] = 1/2 + u[n] - 1/2

This implies

Therefore,

Therefore,

3. Impulse Response
   Consider a system whose impulse response is shown below. Determine and carefully sketch the response of

   this system to the input x [n]=u[n−4].
   Sol) Let the impulse signal be the following.

z-transform

Therefore,

One of the properties is

Therefore,

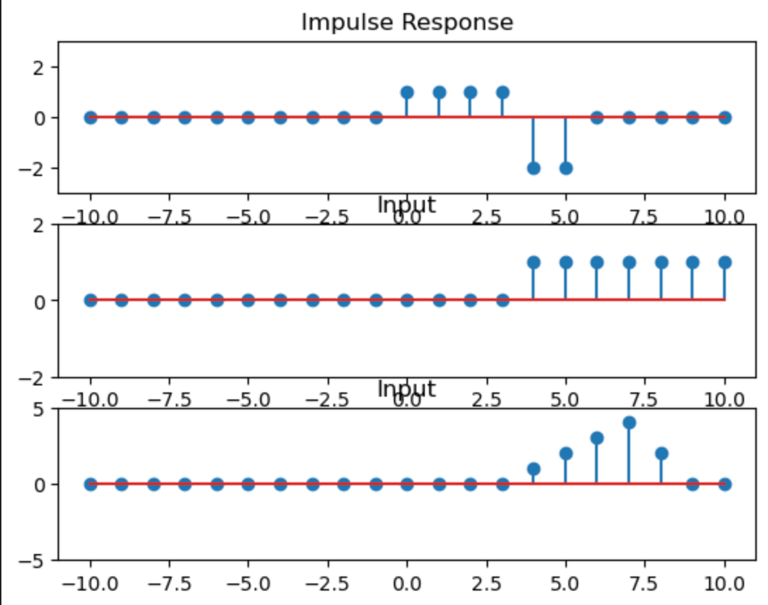
Also determine the causality of the system and its BIBO stability.

4. Series/Parallel
   Calculate the impulse response of the system shown below given that the impulse responses of the processing blocks are
   

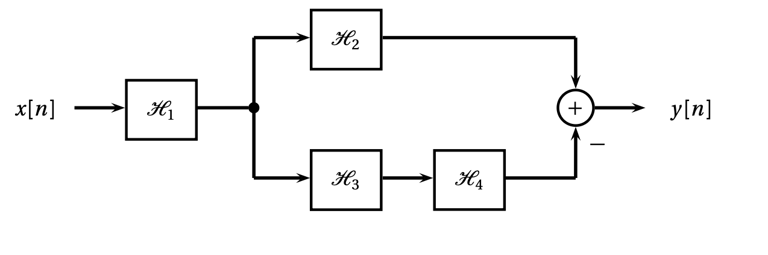
Sol)

This system is casual because of h[n] =0 when n <0

5. System Properties
   For each of the input-output relationships listed below, determine if the corresponding transformation is linear, time-invariant, BIBO stable and causal. For LTI transformations, characterize the corresponding systems by their impulse response.

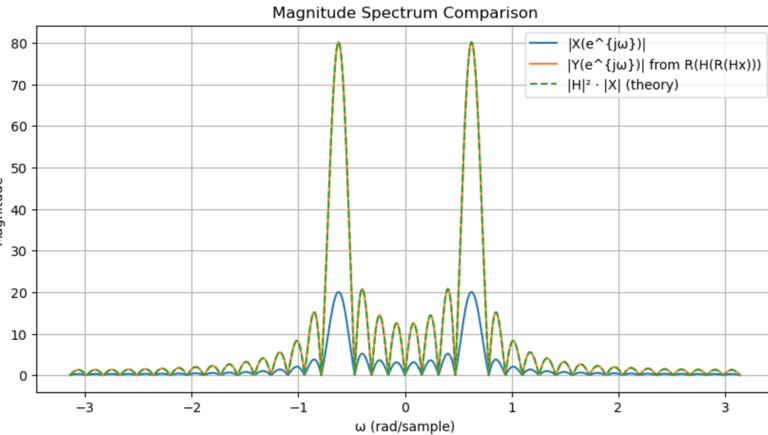
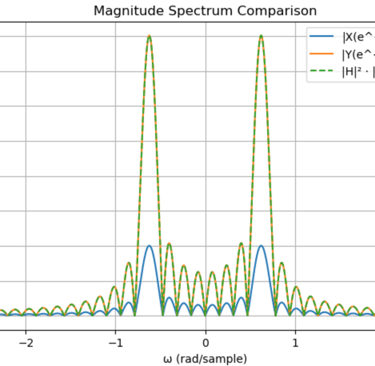
6. Zero Phasing filtering
   Let R be the time reversal operator for sequences so that R{x}[n]=x [−n].

   Let H be a linear time invariant system with a real-valued impulse response. What are the properties of a

   system implementing the following transformation, assuming that the input signal x is real-valued?

   R{H{R{H{x}}}
   Sol)

Since impulse response and x is real-valued, their DTFT are Hermitian-Symmetry, i.e.

This tells you that: the magnitude is even and the phase is odd.

DTFT of the time reversal operator gives us

Therefore,

So, this system gives us zero phase delay and magnitude response equal to the squared magnitude response of the original filter.